Circling Approach

Simulator Environment

Airport / RWY	--
Runway Bearing	--
Surface Wind	--
Wind @ 10000ft	--
ISA Dev	--
Approach Category
この高度で使う風	--

この Environment を使う（滑走路・風・ISA Dev を自動入力する）

滑走路のデータは OurAirports（パブリックドメイン）由来で、 AIP そのものではありません。実運用では必ず最新の AIP／チャートで確認してください。

Simulator で設定を変更

Approach Course から Break して Downwind へ会合し、Base Turn を経て反対側の滑走路へ着陸するまでをまとめて計算します。滑走路方位・Downwind の高度と幅・Cutting Angle を入れると、航跡図・Cut Leg の秒数・Base Turn の諸元が同時に出ます。Bank Angle は Downwind へ会合するための値で、 Base Turn では滑走路にアラインするバンク角を自動で求めます。

Circling Data
Runway Bearing	Field Elevation	Downwind Altitude	Downwind Width	Downwind L/R	ISA Dev
				L R

Airspeed / Bank / Cutting Angle
IAS[kt]	Bank Angle	TAS[kt]	Cutting Angle

Wind
Direction	Speed

Runway Bearing に対する Head/Tail と Cross の内訳は SIM の Environment で、地上風を入れた時点で自動的に出ます。

Base Turn の位置
指定方法	値

Base Turn（最後の旋回）をどこに置くかは、この3つのうちどれか1つを選んで指定します。他の2つはその結果として下のカードと図に表示されます。Downwind 秒数は Abeam から旋回開始までの秒数、Final Align 距離は接地点（TDZ）まで残す Final の直線距離（既定 1.0NM）、末端からの最遠距離は周回中に滑走路末端から最も離れる点までの距離（100m 単位）です。

Input Dataを保存します：

保存したDataを読み込み：

航跡

滑走路を横にとった平面図です。進入側が左、着陸側が右で、 Approach Course（左から進入）→ Break Turn → Cut Leg → Join Turn → Downwind → Base Turn → Final の順に、実際に飛ぶ経路として描いています。入力を変えると図もその場で描き直します。

Approach Category を設定すると保護区域（AIM-J 633b）も重ねます。 旋回する側は制限なしとして末端から半径いっぱいの円弧を、 旋回しない側は障害物があるものとして、末端から中心線に対し 30°・カテゴリー別の距離の点を通る平行線で切った境界を描いています。

Base Turn

Continuous Turn Bank

--°

Runway Align に必要な Bank

計算を実行すると表示します。

Abeam 〜 Base Turn 開始

--秒

計算を実行すると表示します。

Final の直線距離（from THR）

--NM

from TDZ -- NM

この区間を 3° パスで降ります。 TDZ は末端から滑走路内側 1000ft。

Final 開始点の高度

--ft

（-- ft AFE）

計算を実行すると表示します。

Simulator で Approach Category を設定すると、保護区域（AIM-J 633b）に収まっているかを判定します。

Continuous Turn Bank は、Downwind から一定バンクで回り切って滑走路中心線に 沿って出るために必要なバンク角です。入力欄の Bank Angle は Downwind へ会合するためのもので、こちらには使いません。
Downwind と Final は互いに逆コースで、同じ風・同じ IAS なので WCA は同じ量で符号だけ反転します。したがって機首の変向量は 180° ではなく 180° − 2×WCA（解説でいう HDGCHG）です。対気の弧が横に進む距離はその弦の長さ 2R·sin(HDGCHG/2)、進行方向には差し引きゼロで、これに旋回時間ぶんの偏流を足したものが Downwind 幅に等しくなるようバンク角を解いています。
Base Turn の開始点は、接地点まで 1.0NM の Final が取れる位置と定義しています。旋回中も滑走路方向へ流されるので、Abeam から開始点までの距離は Final の直線距離そのものではなく、そのぶん（追い風なら短く、向かい風なら長く）ずれます。
末端から最も遠くなる距離は図の中に橙の点と破線で示しています。旋回中心は中心線から (Downwind 幅 − 旋回半径)、着陸端からは Final の直線距離だけ離れているので、末端から中心へ伸ばした延長が地上航跡と交わる点が最遠になります。保護区域の半径は AIM-J 633b の値（CAT A 1.3 / B 1.5 / C 2.0 / D 2.5 NM）を使っています。これは日本の基準で、ICAO PANS-OPS や FAA TERPS とは異なります。障害物が片側にある場合はその側が制限されるので、実際の適用はチャートと AIP でご確認ください。
Abeam 〜 Base Turn 開始の距離は「Final の直線距離 − 旋回中に滑走路方向へ流される距離」です。対気では進行方向の正味移動がゼロですが、旋回にかかる時間ぶんは風で流されるので、無風と横風のみのときだけ Final の直線距離と一致します。秒数はこれを Downwind の Ground Speed で割ったものです。
Final の直線距離は接地点（TDZ）まで 1.0NM と決めており、これが開始点の定義そのものです。 TDZ は滑走路末端から内側 1000ft（0.16NM）に取っているので、末端（THR）までは 0.84NM になります。高度は THR までの距離を 3° パスで割り戻し、閾値通過高 52ft を足したものなので、 Field Elevation が同じなら風によらず一定です。

Join Downwind

Approach Course から Cutting Angle を取って Downwind 幅へ会合するまでの航法値です。 Cut Leg の距離は、2回の旋回で幅方向へ進む距離（対気の弧＋旋回時間ぶんの偏流）を指定した Downwind 幅から差し引いて求めているので、風があっても指定幅ちょうどに乗ります。そのぶん秒数は風によって変わります。Turn In/Out は考慮していないため、体感的には計算値より 10 秒ほど小さく見積もると合います。

Position	Course	GS [kt]
Approach
Break	TURN	TURN
Cut Leg
Join	TURN	TURN
Downwind

参考表

Downwind 幅・IAS など他の入力はそのままに、風だけを Cross Wind または Head/Tail Wind に振った一覧です。Base Turn Bank は Downwind 幅（Cut Leg で実際に到達する幅ではなく、入力値そのもの）に対して Continuous Turn と同じロジックで解いた値です。

Base Turn Bank — Cross Wind 別

Cut Leg 秒数 — Head/Tail Wind 別

Abeam → Base Turn 開始秒数 — Head/Tail Wind 別

Cross Wind は R が右から・L が左から。Head/Tail Wind は H が向かい風・T が追い風です。

解説

Downwind への会合（Break / Cut Leg）

TAS, Ground Speed, 旋回半径を求める式については他ページを参照してください。

図はイメージです。Approach CourseからLeft Downwindへ入る場合、Right TurnしてCutting AngleθのTrackを取り、一定時間飛行した後、所望のDownwind幅となるようにLeft Turnして会合します。45°のCutting Angleを取る場合、無風では2回の旋回における変針量はそれぞれ45°です。風がある場合はApproach CourseでもCutting LegでもWCAを取ります。Approach CouseとDownwindでは同じCourseなので、やはり2回の旋回における変針量は同じになります。一回の旋回でDownwind方向（Approach Courseに垂直成分）の移動量は図中のaですから、Downwind幅をd、Cutting Angleをθとすると図からわかる通りCutting Legの距離は、

\frac{d - 2 a}{\sin θ}

となります。
次に旋回中の移動距離aについてもう少し考えてみます。
最初の旋回

図はわかりやすいようにApproach CourseのWCAが大きい場合を示しています。点AからBまでLeft Turnを行う場合の対気上の航跡です。ライトブルーで示した風により対地では点CまでDriftされます。点Aから垂直に伸びる点線がApproach Courseです。旋回開始する点Aでは角度(−)αのWCAを取っているため、HeadingがApproach Courseになるまで図では左に膨らんだ形になっていますが、対地ではその間右へDriftされ、航跡はApproach Courseの右側になります。
この旋回A～CにおいてDownwind方向へ移動距離は、Approach Courseに対する垂直成分、線分A'C'です。
図の線分A'B'---(1)
それに旋回にかかった時間ぶんの風のその成分(線分B'C')---(2)
を加えた値です。
角度βは、Cutting Angle（45°または60°）にCutting LegのWCAを加え、Approach CourseのWCA（α）を引いた値です。つまり実際に機首が振れる量（変針量）は Cutting Angle そのものではなく、β−α です。無風なら α=β−Cutting Angle=0 なので変針量はちょうど Cutting Angle に一致しますが、風があるとそのぶんだけ Cutting Angle からずれます。
旋回半径をrとすると、線分A'B' $= r (\cos α - \cos β)$ です。旋回にかかる時間 t は、この実際の変針量 β−α を使って $t = \frac{r (β - α)}{TAS}$ で求まるので、線分B'C' $= t \times WS(x)$ （WS(x): 滑走路方向に対する横風成分）です。
この線分B'C'（旋回中の風によるドリフト）が、以前このページの計算から抜けていました。 Cutting Angle が同じでも、旋回そのものには時間がかかり、その間も風に流され続けるので、強い横風では最大 0.3NM ほど Downwind 幅にきっちり乗らないことがありました。さらに旋回にかかる時間や対気の弧の角度も、Cutting Angle そのもの（α=0 の近似）で計算していたため、そのぶんの誤差も重なっていました。現在は a $= r (\cos α - \cos β) + t \times WS(x)$ として、どちらも近似を使わず計算しています。

Base Turn の Bank 角

まず滑走路方向 (Runway Bearing：下図の垂直) 軸として、その垂直成分（下図の横軸）に注目してみます。Circling中の移動距離は、無風の場合は180°旋回で旋回半径 (R) の2倍 (2R) です。風が存在しているとDownwind、およびFinalではWind Correnction Angle (WCA) を取ることになります。CirclingのBase Turn時にはすでにLanding ConfigurationでありIASは一定ですので、DownwindにおいてもFinal LegにおいてもWCAは同じ量となります。
下図において対気での横方向の移動距離は $- 2 R \cos (HDGCHG)$ となります。(HDGCHG: Heading Chenge 機首変向量)

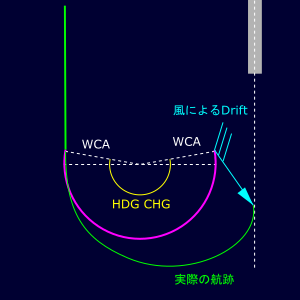
次にDrift量を考えてみます。滑走路方向に対する横風成分[Crosswind Component: WS(x)]により旋回時間 (t) の間にDriftされた距離です。ここでWS(x) をFinalでのWCAを基準にして、左からならマイナス、右からならプラスとします。
ここでLeft Turnなら、滑走路に向かって左から風が吹いている場合はDrift量はプラスとなり、右からならマイナスとなります。Right Turnならそれらは逆になります。
以上のことから2項目を数式化すると、
Left Turnの場合、 $- 2 R \cos (HDGCHG) - t WS(x)$
Right Turnの場合、 $- 2 R \cos (HDGCHG) + t WS(x)$
となり、これがCircling幅 (=d) となればいいのです。
旋回半径を求める式 $R = \frac{V^{2}}{g \tan θ}$ を使ってバンク角を求めます。旋回時間については、上図のMagentaで示した対気の航跡の距離にかかった時間です。HDGCHGをγとします。
航跡は無風の場合180°の円周なので $π R$ 。風がある場合はその比率から $\frac{γ}{180} π R$ となります。これに旋回半径の式を代入すると $\frac{γ}{180} π \frac{V^{2}}{g \tan θ}$ です。これにかかる時間は速さ (V) で割れば算出できます。以上から先に述べた滑走路に対して垂直成分の移動距離(d)を求める式にそれぞれ代入して次の等式を得ます。
$- 2 \frac{V^{2}}{g \tan θ} \cos γ - \frac{γ}{180} π \frac{V}{g \tan θ} WS(x) = d$
$- 2 \frac{V^{2}}{g \tan θ} \cos γ + \frac{γ}{180} π \frac{V}{g \tan θ} WS(x) = d$
バンク角を求めるため、θについて解きます。
Left Turnの場合、 $θ = \arctan (\frac{- 2 V^{2} \cos γ - V γ \frac{π}{180} WS(x)}{g d})$
Right Turnの場合、 $θ = \arctan (\frac{- 2 V^{2} \cos γ + V γ \frac{π}{180} WS(x)}{g d})$